
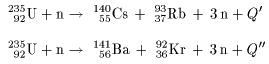
For example, radioactivity measurements are required for accurate monitoring of the damage of tri-structural isotropic (TRISO)-coated particles in the fuel elements of pebble-bed high-temperature gas-cooled reactors (HTGRs), where the fuel pebbles move in the core. Fission gas nuclides are important considerations in the design of radiation monitoring systems and the implementation of radiation protection procedures in nuclear reactors as significant source terms in the primary loop, as these are also reflections of the operation conditions of fuel elements in a reactor core. In the future, the IPRFGN model will be used for calculating fission gas nuclide inventories in various reactors.įission gas nuclides, including the radioisotopes Kr and Xe, are gaseous products of the nuclear fission reaction of fissile material. Based on the application of the IPRFGN model in HTR-10, the results indicate that the proposed IPRFGN model has provided the relationship between the inventories of fission gas nuclides in the core and the reactor conditions in all types of nuclear fission reactors.
#FISSION URANIUM 235 CODE#
The present study findings were consistent with those of a general point–depletion burnup code such as the KORIGEN code. In this study, a simple and efficient model called “Inventories of a Point Reactor for Fission Gas Nuclides” (IPRFGN) was proposed to calculate and interpret such inventories, in which a 10 MW high-temperature gas-cooled experimental reactor (HTR-10) was used as the test case.
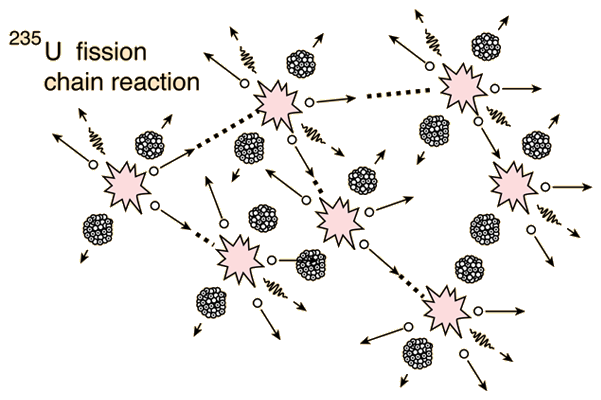
However, there is a niche in which a simple but accurate relationship between reactor conditions and nuclide inventories can reliably predict the fission gas nuclide activities of the reactor core in the primary loop. While uranium-235 is the isotope that undergoes fission it is worth noting that uranium-238 atoms can absorb neutrons to become plutonium-239 which is another atom that can undergo fission.Taking inventories in reactor cores is critical for understanding their radioactive source terms and establishing the relationship between the activity concentration in the primary loop and the status of the reactor core’s fuel. We will consider where the energy comes from in the next section. It is 50 million times more energy than burning the equivalent amount of carbon. The energy released per fission is relatively large.The neutrons may need to be slowed down and are then referred to as thermal neutrons. Both the number and speed of the neutrons is crucial within a working reactor. For fission to occur the neutrons must be going at the right speed – too fast and they will bounce off rather than be absorbed.Once started, fission can become self-sustaining – this is called a chain reaction. The fact that neutrons are also produced means that these neutrons can go on to induce further fissions.These by-products of nuclear power form the majority of the radioactive waste that we will consider next week. Fission products tend to be radioactive.In words this would be: ‘A uranium-235 atom absorbs a neutron to become uranium-236 which then undergoes fission to form the products xenon-140 and strontium-93 with three neutrons.’
#FISSION URANIUM 235 PLUS#
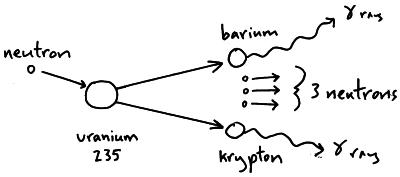
An equation representing this particular fission would be:Ĭap u 92235 postfix times plus n 01 postfix times right arrow cap u 92236 postfix times right arrow times times Xe 54140 postfix times plus times times Sr 3893 postfix times prefix plus of three times n 01 The fission products themselves can vary but examples would be xenon-140 and strontium-93. Neutrons are shown as n 01 using the same notation as for isotopes. This image shoes the particles and types of radiation involved in fission Figure 14 The particles and types of radiation involved in fission


 0 kommentar(er)
0 kommentar(er)
